五年级下册《异分母分数加减法》教学设计

太仓市浮桥镇时思小学 袁艳

教学内容：苏教版小学数学五年级下册第80页例1。

教学目标：

1.通过观察、操作、分析等探究活动，理解异分母分数加减法的算理，掌握异分母分数的加、减法的计算方法，能正确计算简单的异分母分数加、减法，并能用来解决一些简单的实际问题。

2.经历自主探究、实验操作、归纳总结的过程，让学生进一步体会数学知识之间的内在联系，渗透转化思想、数形结合思想，发展数学思考。

3.让学生在交流的过程中体验成功的喜悦，增强学生自主学习、合作交流的意识。

教学重点：探索并掌握计算方法。

教学难点：理解算理。

教学方法：自主探究、质疑引导、讨论交流。

教具学具：长方形纸、彩笔、学习单、多媒体课件。

教学过程：

一、复习导入

1.口算，看谁算得又对又快。

＋+

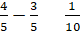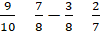追问：这几道口算有什么共同的特点？（都是同分母分数加减法）

计算最后一题时质疑：计算这道分数加法为什么可以把分子相加，分母不变呢？

2.对比引入。

有一块长方形试验田，其中种黄瓜，种番茄，黄瓜和番茄的面积一共占这块地的几分之几？

请一生读题。

提问：这题应该怎样列式？（板书：＋）

引导学生对比，这一题的算式跟刚才我们做的口算有什么不同？揭示课题：异分母分数加减法。

二、探究新知

1.尝试计算，自主探究。

运用已经学过的知识尝试算一算，如果遇到困难，可以利用老师提供的长方形纸折一折、画一画。

2.汇报交流，展示算法。

预设：

（1）+=

（2）+=0.5+0.25=0.75

（3）+=+=

师：对于同学们的这三种算法，你们有什么想法?

生1：第一种算法是把分子加分子，分母加分母。这样做不对，+，和应该比大，可是这样算出的和比小。

生2：第二种算法是把分数化成小数，但是问题是求黄瓜和番茄的面积一共占这块地的几分之几？所以还需要将0.75化成分数。

生3：第三种算法是把异分母分数转化成同分母分数，也就是将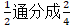，然后再把加上算出。

展示同学的折纸过程，引出数形结合。

3.数形结合，理解算理

同学们都善于思考，大胆说出了自己的想法，到底为什么要先通分再相加呢？我国著名数学家华罗庚曾经说过“数形结合百般好”，下面我们就借助图形来解决这个疑难。

（1）出示长方形纸，折出一张纸的涂上蓝色，再折出这张纸的涂上红色，将两部分合起来看占这张纸的几分之几？怎么知道是？

引导学生明确每一份要一样大，统一了分数单位才可以相加，要把看成，再用+=

（2）如果番茄地占，该怎么算？

学生口答通分过程。

讨论交流：为什么将这块地平均分成6份？这个“6”与原来的分母“2”、“3”有什么关系？课件展示折、涂，引导学生明白平均分成6份之后，每一份都是，统一了分数单位，就可以按照同分母分数加法的方法计算了。把看成，看成，再用+=

4.梳理比较，优化算法

回忆我们的研究过程，说说异分母分数加法可以怎样计算，对比不同的方法，你更喜欢哪种？在小组里说说你的理由。

小组交流，教师巡视参与。

集体交流，明确各种算法的特点，培养学生灵活运用算法。

5.减法验算，算法迁移

用减法验算+=，说说异分母分数减法的计算方法。

6.引导归纳，系统整理。

（1）用自己的话概括异分母分数加减法的计算方法。

（2）师用四个字小结计算步骤。一看，二通，三算，四约

三、巩固应用

1.填一填。（口答）

2.限时两分钟，完成下面各题。

（1）计算下面各题，得到的结果能约分的要约分。

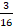
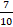+ - 1-

（2）一台拖拉机耕一块地，上午耕了 公顷，下午比上午多耕了 公顷，下午耕地多少公顷？这一天一共耕地多少公顷？

两分钟后集体交流，纠错。最后请同学说说：你想提醒大家计算异分母分数加减法要注意什么。

3.算一算，想一想，计算分数、小数、整数加减法有什么相似之处？

+ = 679-25      1.38+6.2

师小结：异分母分数加减法转化为同分母分数加减法，也就是统一了计数单位，与整数、小数加减法是同样的道理，都是将相同计数单位上的数相加。

四、总结整理

通过这节课的学习你有什么收获？有什么疑问？

五、思维拓展

想一想，括号里可以填哪些分数？

（ ）+（ ）=

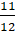
板书设计：

异分母分数加减法

+ = + =

               异分母分数 通分 同分母分数

                                                           转化